My 2009 summer as a research assistant was dedicated to understanding the behavior of dark frames and learning the abilities of the lately improved 14,16, and 24 -inch telescopes at MIT’s Wallace Observatory. In order to be able to specify which project can and should be used with these telescopes, it is important to know the error on magnitude one can expect from each telescope. Learning the properties of dark frames can teach an observer when to subtract dark frames and when it can increase the error on the magnitude. We found that at temperatures below −15⁰, the dark current build up is no longer linear and whether dark frames should be corrected for should be considered on a case to case basis.

In the last year, the telescopes at MIT’s Wallace Observatory went through several signiﬁcant changes. The new mounts have improved the telescope’s tracking, the polishing of the 24-inch telescope mirror has improved its reﬂectivity, and the new cameras increased image resolution. In order to convert these mechanical improvements to scientiﬁc possibilities, we measured the error on the magnitude for the telescope under diﬀerent sky conditions.

Dark frames subtraction is applied to minimize image noise. As the dark frame captures the dark current noise (which normally grows with time), it is custom to expose the dark frame for the same duration as the exposure time of the image. However, if the standard deviation of the dark frame is larger than its mean value, we might achieve a reversed outcome and increase the noise. Therefore, we experimented with diﬀerent camera temperatures and exposures time to learn when we should calibrate for the dark frame.

2.1. Dark Frames

It is a common belief that the longer the exposure you take, the more accumulated dark current you measure. The dark current is a consequence of heat, therefore, it is also important to take the dark frame image at the same temperature as the image you want to later calibrate. Since both light frames and dark frames are taken under the same conditions (temperature and exposure time), the dark frame can be subtracted from the light frame to remove pixels ﬁxed patterns. However, this is not done without cost. Although the dark image maps the pixel-to-pixel dark current variation, it also accumulates random noise. Not only random noise is impossible to

^∗Electronic address: sharon2010@alum.mit.edu

subtract, it also adds up to the noise of the image. The known root-sum-square rule implies a 41% increase in noise level for subtracting one dark frame. To reduce this noise we average several dark frames. Averaging of ×4 dark frames will reduce the noise contribution to half.

2.2. Absolute Magnitude

Absolute magnitude is the apparent magnitude of a star at 10 parsecs away from us. We are measuring the star’s ﬂux received by us and use a comparison star with known apparent magnitude to calculate the apparent magnitude of our target star using the well known formula:

flux2

m1 = m2 +2.5 log₁₀(). (1)

flux1

where m1 and m2 are the magnitudes of the comparison and target star. Using this simple equation, we can measure the faintest star we can observe. As for diﬀerent observing purposes (ex. astrometry vs. photometry), the diﬀerent importance of the error on magnitude, we would most beneﬁt from a correlation between the magnitude and the error on it for diﬀerent ﬁlters.

3. EXPERIMENT

3.1. Dark Frames Analysis

In order to learn the behavior of dark frames we conducted two diﬀerent measurements. The ﬁrst, was measuring the dark current accumulation for a speciﬁc temperature. This was performed by cooling the camera to a previously determined temperature and setting the auto-temperature setting to ’on’. Once the camera reached this temperature and maintained it, we took dark current exposures for several exposure times. As dark frame is the build up of dark current in the image, one would expect it to grow linearly with time. However, we learned that for low temperatures, the camera is cold enough to prevent this charge build. As seen in ﬁgure 1, at a

higher temperature of −5⁰degrees celsius, the dark current grows linearly with exposure time. However, one the temperature is lowered to −15⁰, this linearity is lost.

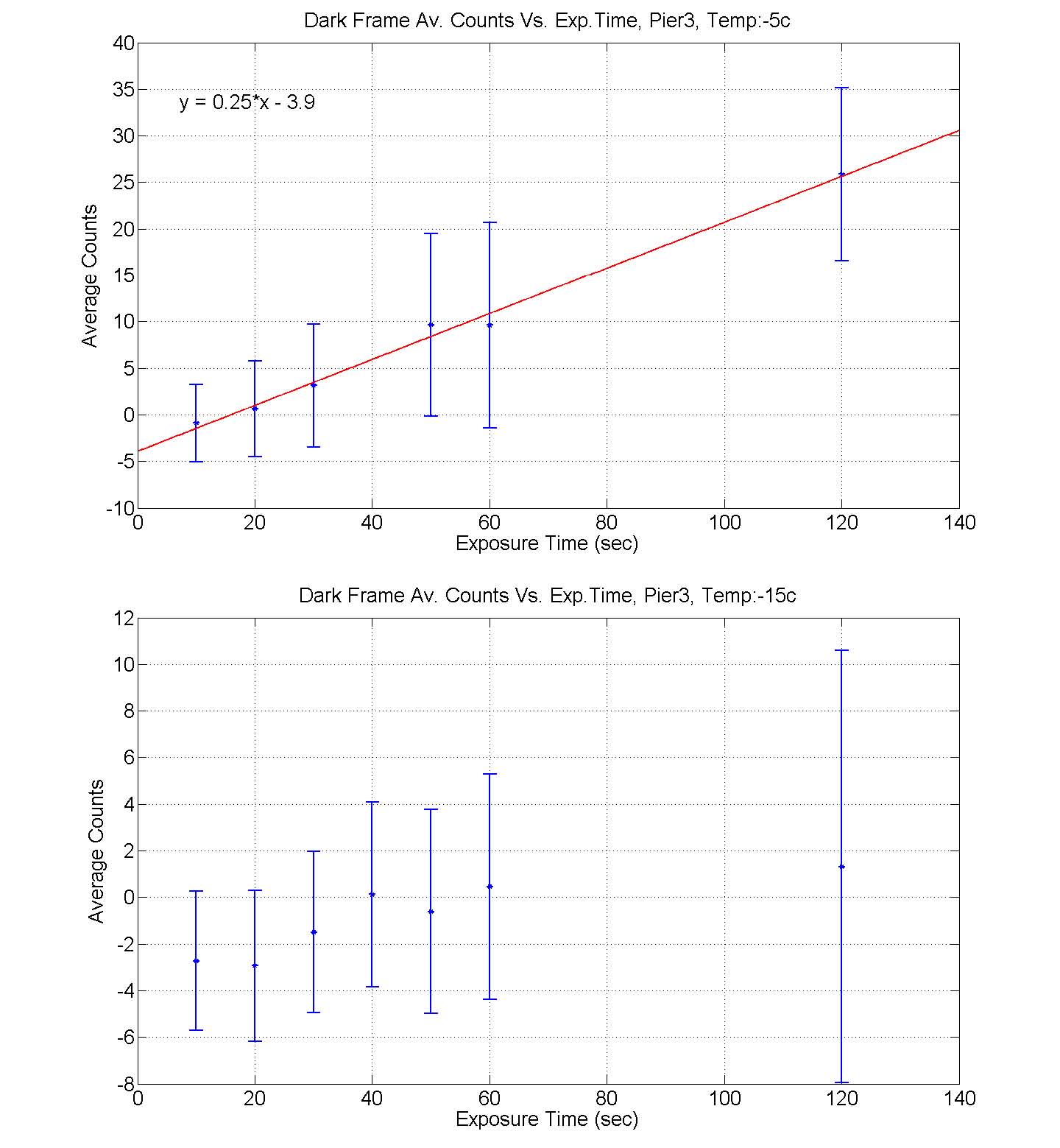
FIG. 1: Average counts Vs. exposure time at −5⁰and −15⁰degrees celsius. The upper plot demonstrates the linearity of the dark frames at high temperatures. As the temperature is lowered to −15⁰(bottom ﬁgure), the linearity is lost. The below zero average is an outcome of the bias subtraction which was applied to all frames.

3.2. Error on Magnitude Analysis

The accuracy of photometry depends on diﬀerent factors as transparency, air mass, magnitude of target star and the calibration of data. As it is hard to predict the inﬂuence of these and other parameters on our error, we experimented with diﬀerent sky conditions to create an estimate on the possible detections. As ﬁgure 2 presents, on a clear night through a 2.6 air mass with a blue ﬁlter, we can predict the error on the magnitude to be 0.39X −6.1. For a brighter night through 1.5 air mass with the same ﬁlter, we predicted the error to be 0.39X − 7.1 which is lower than on a clear night. From this result we can learn the signiﬁcance of the air mass on the predicted error. More results for diﬀerent telescope with diﬀerent ﬁlters on diﬀerent sky conditions can be found on the web https://wikis.mit.edu/confluence/display/WAO/12.410+Project.

4. EXTRA PROJECTS

When observing objects as far as we do, they look circular to us, and we look as a circle to them. In order to interpolate from where

on earth it is possible to observe a 30AU away event, it is necessary to convert a simple drawing of a line on a circle, to an event on the

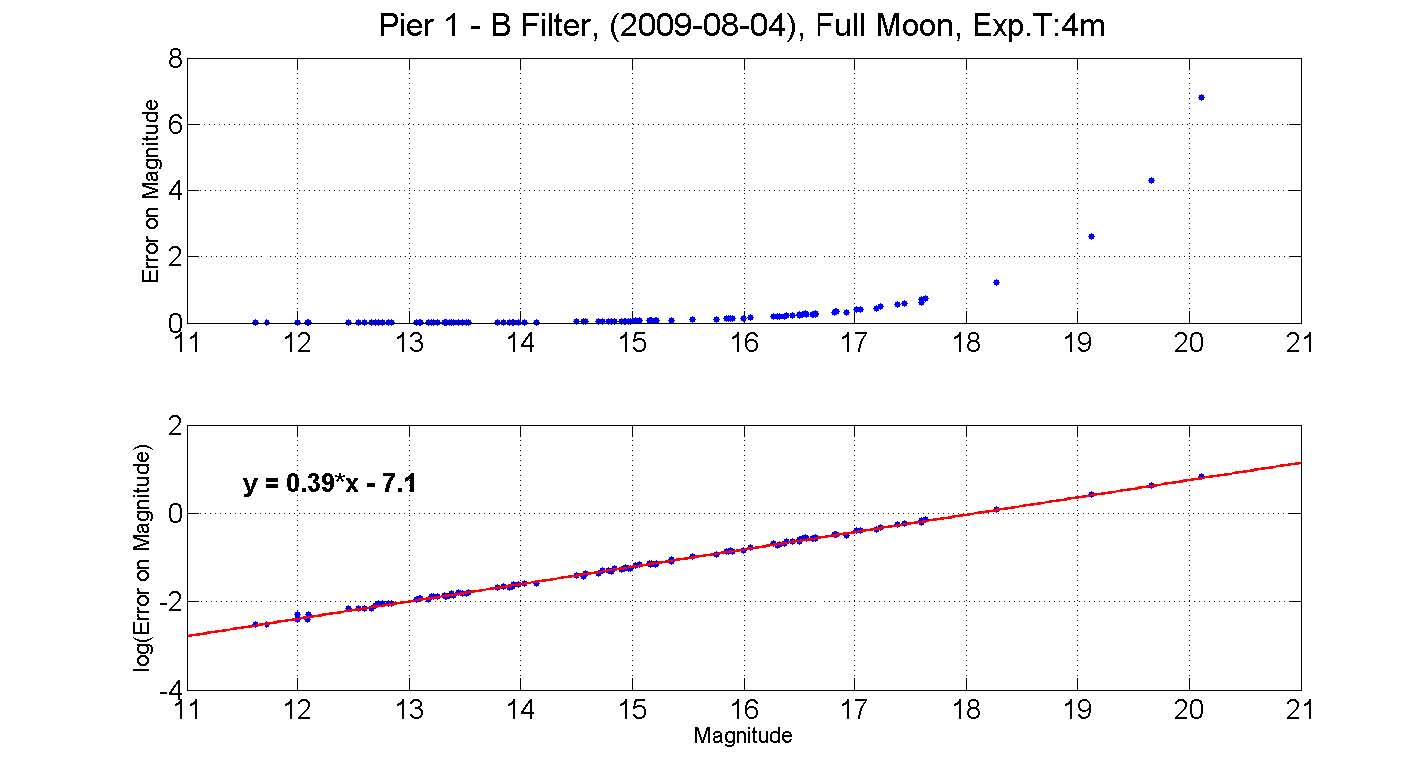
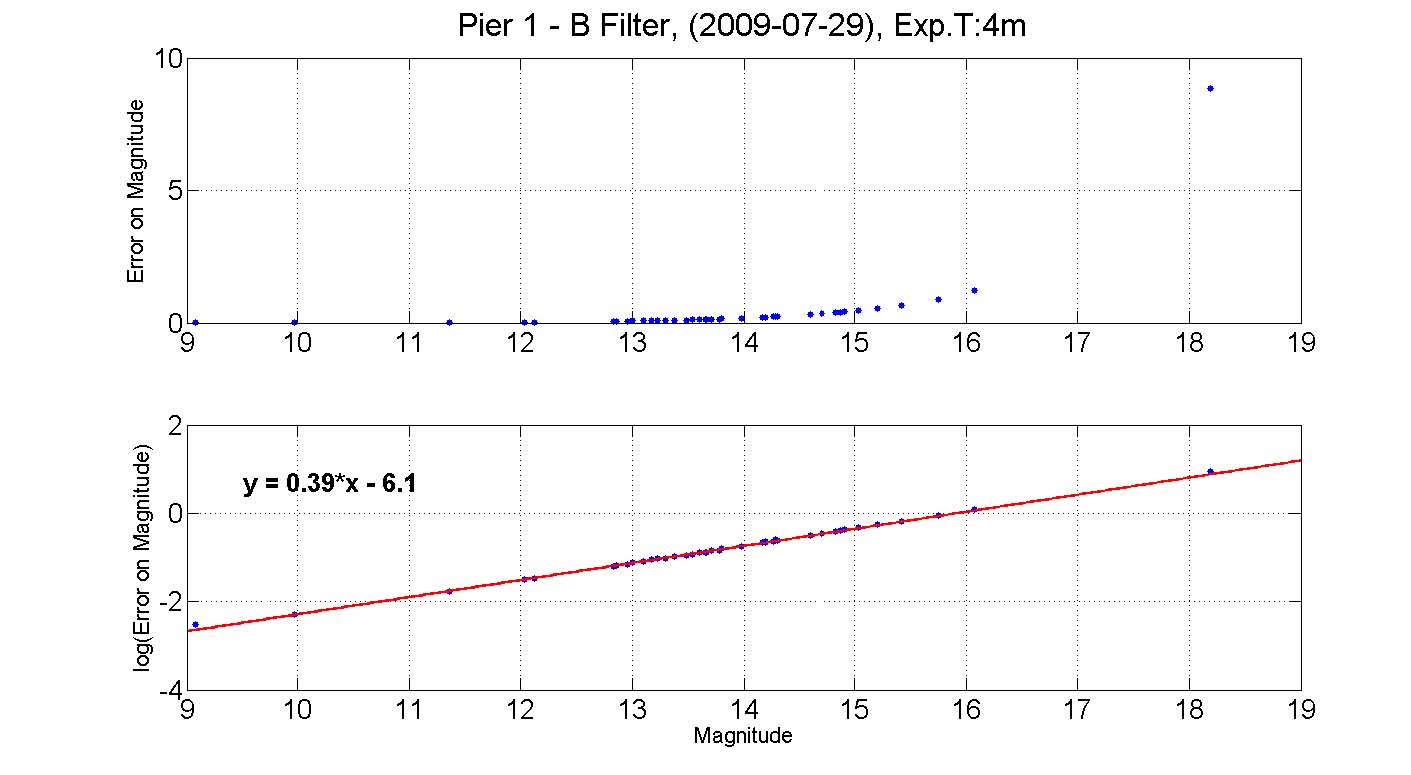
FIG. 2: Error on magnitude vs. magnitude. The data for the upper ﬁgure was taken on a full night, 60 degrees away from the moon (considerably dark), with pier 1, blue ﬁlter, through 1.5 air mass. A plot of the ﬁt to the log10 of the error reveals the magnitude -error relation to be 0.39X − 7.1. The bottom ﬁgure was taken on a dark night with pier 1, blue ﬁlter, through a 2.6 air mass. The magnitude -error relation was found to be 0.39X − 6.1. These results among others that can be found on the Wallace Wiki conﬁrm that the derivative of the error is constant, and the sky condition cause a constant shift in the magnitude -error relation

globe. Therefore, we wrote a MATLAB code which does exactly this. The code takes as inputs the details of a transit as RA and DEC of target, its distance, the position angle and UT mid-time, and outputs the latitudes and longitudes from which it is observable on earth. The code uses the RA, position angle and distance to compute the line equation from which the transit is observable. The UT mid-time is then used to ﬁnd the longitude from which the center of the transit is exactly overhead. When converting from cartesian coordinates to spherical ones, we computed the longitudes and latitudes our imaginary line overlaps.

5. CONCLUSIONS